图3 铸坯温度场计算域和差分网格的建立
2.1 精简差分与完全差分法


与精简差分不同的是,完全差分算法中热物性参数值均采用每个节点在上一时刻所处温度下各自的数值。其具体每个温度下的热物性参数值根据文献[10]中的模型计算来确定。
2.2 多线程串行与并行计算求解
以某厂43m长铸机为例,采用二维传热计算模型节点一般在5000~7000点,以每个切片厚度为100mm计算,正常浇注过程最多存在430片,总共节点数达到215万~301万,在规定的时间(显格式差分稳定性要求的最大时间,例如130ms)已经非常紧迫。此外,每个节点要单独从温度相关的物性参数中查找数据,比精简模型查找耗时要增加4倍,在加上差值算法,更加耗时,串行计算已经达不到要求。并且现在服务器都是多核多线程CPU,串行计算时,仅仅有一核在运行,其他都处于空闲状态。因此有必要利用并行计算。
由式(3)看出,每一点计算值和此点与周围点上一时刻温度相关,此点与周围点并不存在当前时刻的温度交互。故将本研究中的并行计算定义为切片内并行,即首先在片内采用并行计算,算完一片后顺序计算铸机内其他切片,同时对多线程结构进行优化。
多线程串行计算与多线程并行计算效率的比较在相同软硬件环境下测试,串行计算采用精简算法和阶梯函数物性参数,并行计算采用完全算法以及温度相关的曲线形式的物性参数。
以首钢基地某板坯连铸机为测试用例,通过平台数据采集回放器在实验室搭建仿真环境。浇注过程描述如表1所示。
表1串行计算与并行计算测试用例

测试中切片厚度由现场实际使用的0.1m减小到0.05m,整流铸机切片数量从309片增加到618片。每片切片上空间步长为4mm。计算域(四分之一截面)内节点数为226×33=7458。测试最大节点数为7458×618=4609044点。
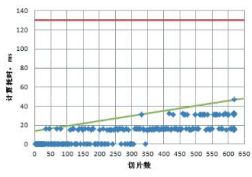
串行计算结果如图4所示。串行计算618片计算耗时125ms,接近根据现有空间步长下差分方程稳定性计算的最大耗时130ms。无法实现有限差分求解温度场完全算法。并行计算计算耗时与切片数量之间的关系如图5所示。618片最大耗时48ms,与同切片数量串行计算耗时的近1/3。由此可见,并行计算可很好地满足完全差分算法。

图4 串行计算测试计算耗时与切片之间关系图