这是对采集到的所有信号数据计算得出的。只要在多个重复周期内计算均方根值,均方根值就与我们计算的时间长短无关。
对于正弦波,均方根值也被定义为:

这意味着,如果平均值为 0,则RMS 值仅为幅度的 0.707 ,这就是正弦波均方根值的众所周知的关系。
但是,如果正弦波有 DC 偏置,则RMS值取决于偏置。事实上,偏置量是正数还是负数都没有关系,rms 值会因正弦波偏置而增加,记住这一点很重要。
通常,当我们想使用RMS 值来表征噪声电平时,尤其是在低电平时,RMS 值可能是一个存在误导性的特征参数。除了我们想要表征的波动之外,噪声中的 DC 分量也会影响RMS 值。这意味着RMS不是噪声水平的良好特征参数。如果我们首先减去平均值然后计算RMS,就可以测量平均值的波动。这正是标准偏差的定义。
标准偏差:标准偏差被定义为:

它是对平均值数据分布的度量。与平均值相比,较大的标准偏差意味着信号在各处都在变化。与平均值相比,较小的标准偏差值意味着信号的变化非常紧密地分布在平均值周围。
在整个采集窗口中,我们首先计算平均值,然后返回计算电压与平均值之差的平方,将所有这些与平均值的偏差平方相加,找到它们的平均值并取平方根。标准偏差的单位还是电压。
标准偏差基本上是减去直流分量的RMS值,标准偏差在一些特殊波形中具有重要意义。当仅有噪声时,RMS是噪声水平的良好表征参数,当我想计算其他恒定信号中的噪声水平时,标准偏差是比RMS 值更好的特征参数。
在值的高斯分布的特殊情况下,信号以平均值为中心,以这种方式计算的标准偏差正是分布的标准偏差。该术语以及平均值是复制高斯分布所需的唯一术语。
在正弦波信号的特殊情况下,标准偏差是正弦波分量的RMS:

其中一些特征参数我们可以快速地从示波器的屏幕读出。而且,事实上,这是重要的第一步,通过设置示波器可以简化这一过程,当我们能够使用 12 位垂直分辨率、高采样率和深存储提取信号的特征参数时,高性能示波器的真正威力就得到了发挥。
在我们的WavePro HD 示波器中,通过使用丰富的内置计算参数计算来计算这些重要的特征参数。
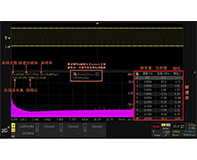
设置完成后,可以在前面的屏幕上显示这些重要的特征参数的值,以及它们的统计数据:平均值、最小值和最大值,甚至它们的标准偏差。以下是从 250k 样本的采集数据中提取的特征参数:

我们应该查看结果,看看它们是否与预期的一致。对于此实例中的正弦波,幅度是峰峰值的½(1.01 V)。我们预计标准偏差值为 0.707x 1.01 V = 0.714 V。我们实际测量的标准偏差为 0.700V。这比我们的预期低2%,这个误差是怎么来的?
我们假设测量的信号是一个理想的正弦波,但事实上,它接近于理想的正弦波,但有点失真。低于预期的标准偏差表明该信号不是理想的正弦波。
使用这些特征参数是需要依据经验的,它们是根据上述定义计算的。我们可以根据待测的信号类型来解释这些值,他们并没有告诉我们关于这个波形的所有信息,只是一些描述它的术语。通过查看频域,我们可以更深入地了解信号。但那将是另一个查看信号的视角。