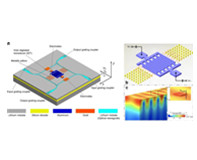
图4.振动检测节点信号链
等式9提供了一个用于估计MEMS加速度计测量总噪声(ANOISE)的关系式,其中使用了噪声密度(φND)和与信号链相关的噪声带宽(fNBW)。

利用等式9中的关系,我们可以估计:当对ADXL357(噪声密度为80 μg/√Hz)使用噪声带宽为100 Hz的滤波器时,总噪声将为0.8 mg (rms)。
用速度衡量振动
某些CBM应用需要用线速度来衡量核心加速度特性(范围、带宽、噪声)。进行这种转换的一种方法是从图1所示简单模型开始,并使用同样的假设:线性运动、单一频率和零平均位移。等式10通过图1中物体瞬时速度(vV)的数学关系式表述了该模型。此速度的幅度(表示为均方根rms)等于峰值速度除以√2。

等式11对此关系求导,得出图1中物体瞬时加速度的关系式:

从等式11中加速度模型的峰值出发,等式12导出了加速度幅度(Arms)与速度幅度(Vrms)和振动频率(fv)的新关系式。

案例研究
现在以ADXL357为例进行研究,将上述内容汇总起来,用线速度表示其范围(峰值)和1 Hz至1000 Hz振动频率范围内的分辨率。图5提供了对本案例有影响的多个特性的图形定义,从ADXL357噪声密度相对于1 Hz至1000 Hz频率范围的关系曲线开始。为了简化讨论,本案例研究中的所有计算均假设全部频率范围内的噪声密度为恒定值(φND = 80 μg/√Hz)。图5中的红色频谱曲线表示带通滤波器的频谱响应,绿色竖直线表示单一频率(fV)振动的频谱响应,其对基于速度估计分辨率和范围会很有用。

图5.研究案例的噪声密度和滤波
此过程的第一步是利用等式9估计四个不同噪声带宽(fNBW)产生的噪声(ANOISE):1 Hz、10 Hz、100 Hz和1000 Hz。表2用两个不同单位的线速度给出了这些结果:g和mm/s2。g在多数MEMS加速度计规格表中相当常见,但振动指标常常不是以此来提供。幸运的是,g和mm/s2的关系已为大家熟知,参见等式13。


本案例研究的下一步是整理等式12中的关系,以导出一个简单的公式(参见等式14)来将总噪声估计(来自表2)转换为线速度项(VRES、VPEAK)。除了提供此关系的一般形式之外,等式14还提供了一个特定例子,其使用10 Hz的噪声带宽(及2.48 mm/s2的加速度噪声,来自表2)。图6中的四条虚线表示所有四种噪声带宽下相对于振动频率(fv)的速度分辨率。