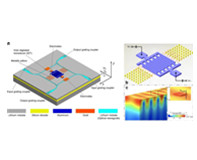
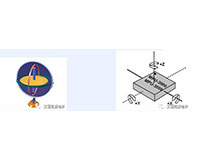
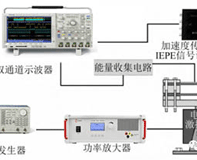
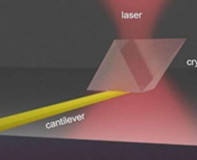
图5. 器件非线性度。
其中:
AMEA为给定gn下的测得加速度。
AFIT 为给定gn下的预测加速度。
多数加速度计或组合器件在给定输入加速度计范围内均存在非线性——例如,30 mg± 2g的范围。对于倾角测量应用,输入坡道斜率在±30°以内,这意味着输出加速度范围在±500 mg (±1g× sin 30°)以内,所以应重新评估该范围内的非线性度。由于非线性度在整个输入范围内是非线性的,所以,很难准确地量化评估这部分误差。然而,由于该器件的数据手册通常都很保守,线性度为30 mg,输入范围为±2g,用10 mg计算±500 mg范围内的误差更合理些。
与初始绝对失调的总失调变化
与初始绝对失调的总失调变化为温度、应力和老化效应导致的失调的最大偏差。该偏差是相对于给定器件的初始绝对失调进行测量的。这是精度总误差的主要贡献因素。
在温度、应力、老化等所有这些因素中,变化与温度在总失调变化中占比很大。一般地,变化与温度曲线是二阶曲线,通常为旋转抛物线。为了消除这部分误差,可以在系统级执行三点校准。对于给定器件,可按下列步骤校准输出失调随温度的变化值。
第1步:
使器件的输出响应以某个 ∆N0值偏移。温度校准流程的第一步是 消除环境温度下的失调。


图7. 第2步:在消除环境温度下的失调之后。
第2步:
接下来,在高温下测试器件,用获得的新信息生成失调校正线性公式。


图9. 第4步:在消除高温下的抛物线旋转分量之后。
第3步:
给现有公式添加一个二阶分量,校正失调剩余部分。设二阶曲线遵循以下公式:

这是二阶抛物线公式,已经通过第1步和第2步消除了旋转分量。
在该公式中,该二阶抛物线有三个解:

然后,我们可以得到温度系数 a, b, c.